Heisenberg's Matrix Mechanics |
|
|
Heisenberg's matrices consist of an array of numbers representing all the possible quantum states of particle or system's individual physical attributes such as energy, position, momentum before and after an event or interaction has taken place. It does not contain any information about why or how this transition takes place. |
|
The rows m represent the initial quantum state. The columns n represent the final quantum state. The matrix can be infinite if m an n run to infinity or finite with limits on m and n
The example opposite is an infinite matrix containing all the frequencies f, emitted by vibrating particles, giving rise to the continuous optical spectrum. |
|
Considering that the momentum p and displacement q of the above particles will also oscillate with the same frequencies, they can therefore also be represented by infinite matrices as shown below. Similar matrices can be developed for other conjugate pairs such as energy and time related to Heisenberg's Uncertainty Principle in quantum mechanics.
In practical applications the degrees of freedom of the particles may be limited so that they may be represented by smaller matrices.
|
|
|
Note that multiplication of matrices is non-commutative which means that pq ≠ qp |
|
pq - qp = (h/2πi) I where:h is Planck's constant, i=√-1 and I is the unit matrix, shown opposite |
|

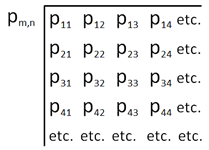

 Heisenberg also developed the following relationship:
Heisenberg also developed the following relationship: