Battery and Energy Technologies |
 |
|
State of Charge (SOC) Determination
Knowing the amount of energy left in a battery compared with the energy it had when it was full gives the user an indication of how much longer a battery will continue to perform before it needs recharging. It is a measure of the short term capability of the battery. Using the analogy of a fuel tank in a car, State of Charge (SOC) estimation is often called the "Gas Gauge" or "Fuel Gauge" function.
See also State of Health (SOH) which represents the long term capability of the battery.
The SOC is defined as the available capacity expressed as a percentage of some reference, sometimes its rated capacity but more likely its current (i.e. at the latest charge-discharge cycle) capacity but this ambiguity can lead to confusion and errors. It is not usually an absolute measure in Coulombs, kWh or Ah of the energy left in the battery which would be less confusing.
The preferred SOC reference should be the rated capacity of a new cell rather than the current capacity of the cell. This is because the cell capacity gradually reduces as the cell ages. For example, towards the end of the cell's life its actual capacity will be approaching only 80% of its rated capacity and in this case, even if the cell were fully charged, its SOC would only be 80% of its rated capacity. Temperature and discharge rate effects reduce the effective capacity even further. This difference in reference points is important if the user is depending on the SOC estimation as he would in a real gas gauge application in a car. Unfortunately the SOC measurement reference is often defined as the current capacity of the cell instead of the rated capacity. In this case a fully charged cell, nearing the end of its life, could have an SOC of 100% but it would only have an effective capacity of 80% of its rated capacity and adjustment factors would have to be applied to the estimated capacity to compare it to its rated new capacity. Using the current capacity rather than the rated capacity is usually a design shorcut or compromise to avoid the complexity of determining and allowing for the age related capacity adjustments which are conveniently ignored.
Basing the SOC estimate on the current capacity of the battery rather than its rated capacity when new is equivalent to progressively reducing the capacity of the fuel tank over the lifetime of the vehicle without informing the driver. If an accurate estimate of the charge remaining in the battery is required the ageing and environmental factors must be taken into account.
For cell balancing applications, it is only necessary to know the SOC of any cell relative to the other cells in the battery chain. Since all the cells will have been subject to the same influences during their lifetime, the ageing and environmental adjustments, which apply equally to all cells, can be ignored for this purpose.
SOC Accuracy RequirementsA knowedge of the SOC is particularly important for large Lithium batteries. Of all the common cell chemistries Lithium is the most chemically reactive and the only one which needs electronic battery management systems (BMS) to keep the battery within a safe operating window and to ensure a long cycle life. Control of the SOC is a major function of the BMS. Furthermore, automotive applications, one of the main uses of large Lithium batteries, need very precise control of the SOC for efficient and safe management of the energy flows.
See Estimation Accuracy possibilities below
Methods of Determining the State of ChargeSeveral methods of estimating the state of charge of a battery have been used. Some are specific to particular cell chemistries. Most depend on measuring some convenient parameter which varies with the state of charge.
Direct Measurement This would be easy if the battery could be discharged at a constant rate. The charge in a battery is equal to the current multiplied by the time for which it flowed. Unfortunately there are two problems with this. In all practical batteries, the discharge current is not constant but diminishes as the battery becomes discharged, usually in a non-linear way. Any measurement device must therefore be able to integrate current over time. Secondly, this method depends on discharging the battery to know how much charge it contained. In most applications except perhaps in qualification testing, the user (or the system) needs to know how much charge is in the cell without discharging it.
It is not possible either to measure directly the effective charge in a battery by monitoring the actual charge put into it during charging. This is because of the Coulombic efficiency of the battery. Losses in the battery during the charge - discharge cycle mean that the battery will deliver less charge during discharge than was put into it during charging. The Coulombic efficiency or charge acceptance is a measure of how much usable energy is available during discharging compared with the energy used to charge the cell. Charge efficiency is also affected by temperature and SOC.
SOC from Specific Gravity (SG) Measurements This is the customary way of determining the charge condition of lead acid batteries. It depends on measuring changes in the weight of the active chemicals. As the battery discharges the active electrolyte, sulphuric acid, is consumed and the concentration of the sulphuric acid in water is reduced. This in turn reduces the specific gravity of the solution in direct proportion to the state of charge. The actual SG of the electrolyte can therefore be used as an indication of the state of charge of the battery. SG measurements have traditionally been made using a suction type hydrometer which is slow and inconvenient. Nowadays electronic sensors which provide a digital measurement of the SG of the electrolyte can be incorporated directly into the cells to give a continuous reading of the battery condition. This technique of determining the SOC is not normally suitable for other cell chemistries.
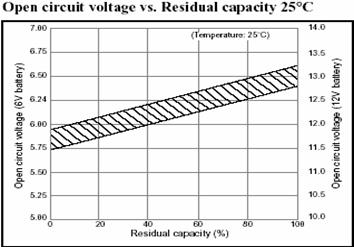
Voltage Based SOC Estimation This uses the voltage of the battery cell as the basis for calculating SOC or the remaining capacity. Results can vary widely depending on actual voltage level, temperature, discharge rate and the age of the cell and compensation for these factors must be provided to achieve a reasonable accuracy. The following graph shows the relationship between the Open Circuit Voltage and the Remaining Capacity at constant temperature and discharge rate for a high capacity Lead Acid cell. Note that the cell voltage diminishes in direct proportion to the remaining capacity.
Lead Acid Battery
Problems can occur with some cell chemistries however, particularly Lithium which exhibits only a very small change in voltage over most of the charge/discharge cycle. The following graph shows the discharge curve for a high capacity Lithium-ion cell. This is ideal for the battery application in that the cell voltage does not fall appreciably as the cell is discharged, but for the same reason, the actual cell voltage is not a good measure of the SOC of the cell.
The rapid fall in cell voltage at the end of the cycle could be used as an indication of imminent, complete discharge of the battery, but for many applications an earlier warning is required. Fully discharging Lithium cells will dramatically shorten the cycle life and most applications will impose a limit on the DOD to which the cell is submitted in order to prolong the cycle life. While the cell voltage can be used to determine the desired cut off point, a more accurate measure is preferred for critical applications.
See also how measuring the cell voltage during "rest periods"can improve the accuracy of the estimates of the SOC in Lithium batteries on the Software Configurable Battery page. Current Based SOC Estimation - (Coulomb Counting) The energy contained in an electric charge is measured in Coulombs and is equal to the integral over time of the current which delivered the charge. The remaining capacity in a cell can be calculated by measuring the current entering (charging) or leaving (discharging) the cells and integrating (accumulating) this over time . In other words the charge transferred in or out of the cell is obtained by accumulating the current drain over time. The calibration reference point is a fully charged cell, not an empty cell, and the SOC is obtained by subracting the net charge flow from the charge in a fully charged cell. This method, known as Coulomb counting, provides higher accuracy than most other SOC measurements since it measures the charge flow directly. However it still needs compensation to allow for the operating conditions as with the voltage based method.
Three current sensing methods may be used.
Coulomb counting depends on the current flowing from the battery into external circuits and does not take account of self discharge currents or the Coulombic efficiency of the battery.
Note that in some applications such as automotive batteries the "continuous" battery current is not monitored. Instead the current is sampled and the continuous current is reconstructed from the samples. In such cases the sampling rate must be fast enough to capture the current peaks and troughs associated with the acceleration and regenerative braking corresonding to the user's driving style.
SOC Estimation from Internal Impedance Measurements During the cell charge - discharge cycles the composition of the active chemicals in the cell changes as the chemicals are converted between the charged and discharged states, and this will be reflected in changes to the cell impedance. Thus measurements of cell internal impedance can also be used to determine SOC however these are not widely used due to difficulties in measuring the impedance while the cell is active as well as difficulties in interpreting the data since the impedance is also temperature dependent. Fuzzy Logic and other similar models have been used to overcome these problems and ASICs have been developed for this purpose.
Other State of Charge Measures With a constant load and constant ambient conditions, Lithium cells have a linear SOC discharge characteristic over time which could possibly allow the SOC to be determined from running time, or in the case of a pure electric vehicle, distance travelled. This method depends on maintaining a constant driving pattern and major inaccuracies will be introduced if the driving pattern changes. It can also not be applied when intermittent charging is involved as with HEVs. While the measure may not be suitable as a basis for BMS in automotive use, it could be used for simple applications such as bicycle range indicators and it could also provide a verification check of the BMS model predictions for safety purposes.
Factors Influencing the State of Charge in Lithium BatteriesUnfortunately neither voltage measurement nor coulomb counting alone is sufficient for high accuracy fuel gauging because the charge a cell is able to accept or deliver depends not just on the fundamental cell design but also on both the age of the cell and its short and long term operating environment.
Usable Capacity SOC estimations for Lithium cells are complicated by the fact that the useable capacity of a cell is not constant but varies significantly with temperature, the charge discharge rates and with the age of the cell and lesser effect with other parameters such as the time between charges (due to the self dischage rate).
Charge - Discharge Rates The effective capacity of a cell depends on the rate at which it is charged and discharged as illustrated in the graph on Discharge Rates. This is because the electrochemical actions in the cell take a finite time to complete and they can not follow instantaneously the electrical stimulus or load placed on the cell. This is explained in the section on Charging Times. If a cell is subject to short term charging and discharging pulses, as in EV and HEV applications, the chemical effect of a charging pulse may not be fully completed before the subsequent discharge pulse starts to reverse the process. Even with coulomb counting this can lead to errors in determining the SOC of the cell unless the rates of the chemical actions are taken into account.
Hysteresis At the same state of charge, the open circuit voltage (OCV) following a charge is higher than the OCV following discharge. This is another manifestation of the time constant associated with the delay in the battery chemical reaction in keeping up with electrical stimulus.
See more about hysteresis and how it affects the accuracy of SOC measurements.
Temperature and Discharge Rate The following graph shows how the capacity of a Lithium cell varies with temperature and discharge rate. It shows that at normal working temperatures the coulombic efficiency of the cell is very high, but at low temperatures there is a major drop in efficiency particularly at high discharge rates which can give rise to serious errors in the estimation of the SOC. This phenomenon is not peculiar to Lithium cells as other cell chemistries also demonstrate a deterioration in performance at low temperatures.
The graph shows a Lithium cell working between its specified upper and lower voltage cut -off limits of 4.2.Volts and 2.5 Volts respectively. These are considered the fully charged and the empty conditions of the cell. The "Full" line is the point at which the cell reaches full charge using the constant current - constant voltage charging method at the corresponding temperature. Two "Empty" lines are shown corresponding to two different discharge rates 0.2C and 1.0C. The capacity of the cell at a given rate and temperature is the difference from the "Full" line and the corresponding "Empty" line. In actual practice, the cell may be charged at one temperature and discharged at a different temperature and this must be taken into account when calculating the effective capacity of the cell. Note that the cell is very inefficient at giving up its charge at high discharge rates and low temperatures. In other words, its coulombic efficiency deteriorates dramatically at low temperatures. Note also that the cell above could be fully discharged at the high current rate yet could be further discharged at the low current rate by the number of milliamp-hours between the two "Empty" points that correspond to the present cell temperature.
Typical cell specifications only give the capacity at 25 ºC and 0.3 C rate. The graph below shows the combined effect of rate and temperature on the effective cell capacity. Note that the available capacity is reduced at high discharge rates and though there is a slight capacity reduction when operating at high temperatures, there is a substantial reduction at low temperatures. Similar effects come into play during the charging cycle.
The above graph characterises the performance of a Lithium cell over two of its expected operating conditions. The matrix of capacity values associated with all the possible current-temperature combinations is useful as a look up table used by charge estimation algorithms below. This battery performance matrix is similar to an "engine map" which stores a plurality of engine performance curves under different operating conditions used in the control systems employed modern internal combustion engines.
The graph below shows how ageing affects the cell capacity. To account for this, the formulas for calculating remaining capacity must be capable of dynamically changing over time to remain accurate.
The cycle life of a cell is usually considered complete when the cell capacity has fallen to 80% of its value when the cell was new. Note that the capacity reduces in a fairly linear way as the cell ages and continues to do so after specified battery lifetime. There is no sudden death and batteries can continue to be used albeit with a reduced capacity.
Self Discharge In addition to the charge being put into and taken out of the battery during the normal charge - discharge process, the continuing long term effect of self discharge consuming the available energy in the cell must also be taken into account.
Other Factors Other factors such as charge/discharge efficiency also affect the cell capacity.
Calculating the SOC of Lithium BatteriesAs noted above, voltage or current measurements can provide a rough indication of the SOC of a battery, but for more precision, particularly for Lithium batteries, other factors must be taken into account.
Theoretical SOC Estimation It is possible but not necessarily practical to estimate the SOC of a battery from purely theoretical considerations. Batteries are non-linear. The SOC could be calculated from measured cell parameters and operating conditions if sufficient data were available. Unfortunately this is far too complex since there are 30 or more variables affecting cell performance some of which are much more significant than others. They are listed below for information only since this method is not used in practice (unless in a severely cut down form)'
A theoretical calculation of the SOC will always be limited by number of effects for which equations can be developed.
Practical SOC Estimation Alternatively the performance characteristics of a typical sample cell (or cells) can be measured and the results used as a template to represent the performance of the rest of the population. Basing the cell performance estimates on look up tables constructed from measured data from actual cells is much simpler than carrying out theoretical estimates since it automatically takes account of most if not all the factors affecting the SOC. Look up tables are stepwise approximations of the performance response curves which represent the cell discharge performance as a function of temperature, discharge rate or other parameters. See example above. The necessary look up tables are developed from laboratory measurements under controlled conditions. The process of gathering the data and constructing the look up table is called cell characterisation and only needs to be carried out once, however a new data set or look up table must be produced for each cell chemistry variant and cell construction used. Reusable, standard, software can be used to accommodate different data sets
Once the cells have been characterised the next step is to consider the battery application. Coulomb counting is used to provide an intial estimate of the cell SOC and this value is then modified to take account of the cell's unusable capacity corresponding to its operating point by referring to the look up table. Thus the SOC estimation is accomplished by building a model of the battery which replicates the battery characteristics in software and an algorithm which predicts its behaviour in response to various external and internal conditions. This method of course needs sensors to provide the measurement data of the current battery status, memory to store the battery model and a microprocessor to calculate the results.
Sensors in the battery provide analogue inputs representing temperatures, cell voltages and currents to the model and precision A/D converters translate these inputs into digital form. Further information such ambient temperatures and the status of various alarms if necessary can also be provided to the model. These inputs are constantly monitored and updated at the request of the microprocessor which controls the model. The model can then use these inputs to estimate the SOC, or other, status of the battery at any instant in time.
In dynamic applications such as automotive batteries, inputs must be monitored at least once per second to ensure that no significant charge flows or critical events are missed and the SOC prediction for every individual cell in the battery must be completed during the sampling interval. Because of the complexity of the algorithm and the number of inputs involved the system must perform over a million or more floating point calculations per second. This requires a powerful microprocessor. An example of the need for continual updating of SOC estimations in a working system is given in the section on Battery Management Systems.
Estimation Accuracy of SOC Estimates Based on Look Up Tables
For an accurate representation of the charge / discharge characteristics of the cell, similar look up tables must be developed for all the known factors which significantly affect the cell capacity (Ah) and impedance, such as cell temperature, ambient temperature, charge and discharge rates, heat dissipation rates, the cell self discharge rate charge or coulombic efficiency and the capacity degradation over the lifetime of the cell. If any of the key parameters which affect the usable capacity of the cell are ignored, there will be a correspondingly large offset error in the SOC estimation. SOC offset errors based on Coulomb counting alone, without the compensating factors, can be as high as 30%! Accuracy may be limited by the small sample size used for constructing the data set and whether the samples used to characterise the cells were truly representative of the population throughout the expected production run of the cells. Accuracy will also depend directly on the number of data points in the look up table. Various algorithms (examples below) have been developed to provide more accurate estimations from limited data sets. Essentially this means joining up the measured performance points in the data set or look up table into a continuous surface to enable performance values to be extracted from intermediate points. These algorithms each have their own characteristic estimation accuracy. Coulomb counting is also subject to errors since all the Coulombs pumped into the battery during charging can not be converted into available charge. Some of the energy is inevitably lost in the chemical conversion process usually as heat. Similarly on the return trip, for the same reasons, some of the available charge is lost and only part of the stored charge is available for doing work. The round trip energy loss is about 3% for a Lithium battery. The Coulombic efficiency is the ratio between the discharge energy and the charging energy. Another reason why all the energy put into the battery is not available to come out again is the self discharge of the cells. Self discharge of Lithium batteries is typically less than 3% per month so for periods of a day or so the effect is very small but it becomes more significant the longer the periods between charging and can be the source of accumulating errors unless the battery monitoring circuit is regularly reset or calibrated. Random errors arrise from the inaccuracies in involved in measuring the factors which are actually taken into account in the SOC estimation. This applies to the cell characterisation as well as to the cells in the operating batteries, thus there are two potential sources of similar errors. Typically the net effect of a series of random errors such as those due to measurement inaccuracies can be calculated using the "Root Sum of Squares" method . Over time the system "fully charged" reference point of the battery may drift so the system should be calibrated regularly to reset the reference SOC to 100% when the battery is fully charged. Regular calibration of the SOC estimation system is needed to avoid a cumulative error build up. This is particularly true for HEV batteries which under normal circumstances never reaches their fully charged condition when the system can be reset to a known level of charge.
Taking all these factors into consideration the SOC calculation could be subject to very large errors which could jeopardise the application unless steps are taken in the battery system design to mitigate these errors. The accuracy claimed for SOC calculation should be consistent with the combined measurement accuracies of the contributing parameters plus any offset errors. Manufacturer's claims of SOC accuracy of better than 5% are typical but this seems hard to justify considering the factors outlined here and errors may diverge even more as the cells grow older. Compare this with the Accuracy Requirements above
Several different techniques such as Fuzzy Logic, Kalman Filtering, Neural Networks and recursive, self-learning methods have been employed to improve the accuracy of the SOC estimation as well as the estimation of state of health (SOH).
Fuzzy Logic is simple way to draw definite conclusions from vague, ambiguous or imprecise information. It resembles human decision making with its ability to work from approximate data to find precise solutions. Unlike classical logic which requires a deep understanding of a system, exact equations, and precise numeric values, Fuzzy logic allows complex systems to be modelled using a higher level of abstraction originating from our knowledge and experience. It allows expressing this knowledge with subjective concepts such as big, small, very hot, bright red, a long time, fast or slow. This qualitative, linguistic representation of the expert knowledge presents a natural rather than a numerical description of a system and allows relatively easy algorithm development compared to numerical systems. The outputs can then be mapped into exact numeric ranges to provide a characterisation of the system. Fuzzy logic is used extensively in automatic control systems. Using this technique we can use all the information available to us about the performance of a battery to derive a more accurate estimation of its state of charge or the state of health. Software packages are available which simplify this process.
Kalman filtering addresses an age-old question: How do you get accurate information out of inaccurate data? More pressingly, How do you update a "best" estimate for the state of a system as new, but still inaccurate, data pour in? An HEV automotive application is an example of this situation. The battery SOC is affected by many simultaneous factors and is continually changing due to the user driving pattern. The Kalman filter is designed to strip unwanted noise out of a stream of data. It operates by predicting the new state and its uncertainty, then correcting this with a new measurement. It is suitable for systems subject to multiple inputs and is used extensively in predictive control loops in navigation and targeting systems. With the Kalman Filter the accuracy of the battery SOC prediction model can be improved and accuracies of better than 1% are claimed for such systems. As with Fuzzy Logic, standard software packages are available to facilitate its implementation.
A Neural Network is a computer architecture modelled upon the human brain's interconnected system of neurons which mimics its information processing, memory and learning processes. It imitates the brain's ability to sort out patterns and learn from trial and error, discerning and extracting the relationships that underlie the data with which it is presented.
Each neuron in the network has one or more inputs and produces an output; each input has a weighting factor, which modifies the value entering the neuron. The neuron mathematically manipulates the inputs, and outputs the result. The neural network is simply neurons joined together, with the output from one neuron becoming input to others until the final output is reached. The network learns when examples (with known results) are presented to it; the weighting factors are adjusted on the basis of data - either through human intervention or by a programmed algorithm-to bring the final output closer to the known result. In other words, neural networks "learn" from examples (as children learn to recognise dogs from examples of dogs) and exhibit some capability for generalisation beyond the training data.
Neural networks thus resemble the human brain in the following two ways:
The true power and advantage of neural networks lies in their ability to represent both linear and non-linear relationships and in their ability to learn these relationships directly from the data being modelled. Among the many applications are predictive modelling and control systems.
Neural Network techniques are useful in estimating battery performance which depends on quantifying the effect of numerous parameters most of which can not be defined with mathematical precision. Algorithms are refined with the aid of experience gained from the performance of similar batteries.
Two Parameter SOC Estimation and Accuracy Improvement While the cell voltage variation with SOC alone is not large enough to provide an accurate measure of the SOC, it is however sufficient to provide an error checking reference for current derived (Coulomb counting) SOC estimations. Furthermore, since the accuracy of the SOC determined by Coulomb counting depends on applying adjustment factors depending on the measured battery rate, temperature and voltage, the same voltage measurements can be used to provide an alternative estimation of the SOC without appreciably affecting the complexity of the system. The overall accuracy of the SOC estimation can then be improved by combining suitably weighted values of the current and voltage based SOC estimations into a single value.
Consumer Battery Condition IndicatorsSmall primary cells are now available with a on-cell analogue SOC indicators known as battery testers or fuel gauges. On the side of the cell they incorporate a printed strip resembling a thermometer which provides a rough indication of the remaining capacity in the battery. Based on thermochromic and conductive inks, a thin layer of conductive ink is applied in a wedge shape. The narrowest point indicates the lowest charge level and the widest area indicates a full charge. When the circuit is completed and current flows through the conductive ink and the resistance of the ink causes it to heat up. A small amount of current can generate enough heat to affect the smallest area of the wedge but as the area widens more current is needed to raise its temperature. The thermochromic ink printed on top of the conductive ink changes colour depending on the temperature and the extent of the colour change along the wedge indicates the magnitude of the current and hence the battery voltage. The design is completed with a masking layer of normal ink which provides the illusion of a thermometer or analogue fuel gauge. The measurement accuracy is dependent on the ambient temperature.
SOC of CapacitorsThe state of charge of a capacitor is represented by the voltage across its terminals.
Battery Life and SOCSee more about how operating SOC affects battery life.
|
|||||||||||||||||||||||||||||
![]() Print This Page || Home || FAQ || Site Map || Legal || Privacy Promise || Contacts
Print This Page || Home || FAQ || Site Map || Legal || Privacy Promise || Contacts
Woodbank Communications Ltd, South Crescent Road, Chester, CH4 7AU, (United Kingdom)
Copyright © Woodbank Communications Ltd 2005